Vorhilfe - Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen
URL: http://www.mathe-raum.de/vorkurszettel?id=66
| Sigrid Sprock Marc O. Sandlus | www.matheraum.de Vorbereitung auf das Zentralabitur in Mathematik in NRW Aufgabenblatt 9 Abgabe: So 03.02.2008 09:00 | 27.01.2008 |
| Aufgabe 1 | ||
|
Aufg.-Nr.: 24 Bereich: vektorielle Geometrie Kursart: LK WTR Dreieckspyramide Gegeben sind die Punkte A(- 6; 8; 7 ), B(- 3; - 4; 4), C(1 ;- 8 ;6 ) und D(9 ;- 4 ;- 2). a) Ermitteln Sie die Koordinatenform der Ebene E, die durch die drei Punkte A, B und C gegeben ist. ( mögliches Ergebnis: 2x + y - 2z = - 18) b) Geben Sie die Schnittpunkte Koordinatenachsen an und zeichnen Sie das Dreieck Koordinatensystem ein. ( 1 LE = 0,5 cm, Verkürzungsfaktor in x-Richtung c) Zeigen Sie, dass der Punkt D außerhalb der Ebene E liegt und berechnen Sie den Abstand des Punktes D von der Ebene E. d) Ermitteln Sie die Koordinaten des Punktes D, den man durch Spiegelung des Punktes D an der Ebene E erhält. e) Bestimmen Sie den Flächeninhalt des Dreiecks ABC sowie das Volumen der Dreieckspyramide, die das Dreieck ABC gemeinsam mit dem Punkt D bildet. f) Durch 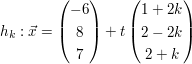 ist eine Geradenschar mit dem gemeinsamen Punkt A gegeben. Zeigen Sie, dass alle Geraden der Schar in der Ebene E liegen. ist eine Geradenschar mit dem gemeinsamen Punkt A gegeben. Zeigen Sie, dass alle Geraden der Schar in der Ebene E liegen.
g) Entscheiden Sie, ob die Gerade AC eine Gerade der obigen Geradenschar hk ist. h) Berechnen Sie den Schnittwinkel, den die Gerade AC mit der Geraden Zusammengestellt von den Fachdezernenten Mathematik der 5 Bezirksregierungen in NRW 33 | ||
© Copyright 2003-25 www.vorhilfe.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.