injektivDefinitionen von injektiv, surjektiv, bijektiv
Seien 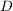 und und 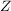 nichtleere Mengen. Sei nichtleere Mengen. Sei 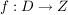 eine Funktion mit dem Definitionsbereich eine Funktion mit dem Definitionsbereich 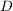 und dem Zielbereich und dem Zielbereich 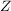 . .
Die Funktion  heißt: heißt:
- injektiv, falls für alle 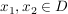 mit mit 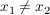 stets stets  gilt gilt
(äquivalent dazu:  heißt injektiv, falls für alle heißt injektiv, falls für alle 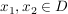 aus aus  stets auch stets auch 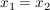 folgt .) folgt .)
- surjektiv, falls für alle 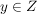 (mindestens) ein (mindestens) ein 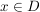 mit mit  existiert existiert
(äquivalent dazu:  heißt surjektiv, falls heißt surjektiv, falls 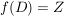 gilt. Hierbei ist gilt. Hierbei ist  der Bildbereich der Funktion der Bildbereich der Funktion  .) .)
- bijektiv, falls  sowohl injektiv als auch surjektiv ist. sowohl injektiv als auch surjektiv ist.
Beispiele.
1.) Die Funktion 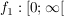 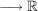 definiert durch definiert durch 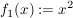 ist injektiv, nicht aber surjektiv (also insbesondere nicht bijektiv). ist injektiv, nicht aber surjektiv (also insbesondere nicht bijektiv).
2.) Die Funktion 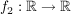 definiert durch definiert durch 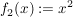 ist weder injektiv noch surjektiv (also insbesondere nicht bijektiv). ist weder injektiv noch surjektiv (also insbesondere nicht bijektiv).
3.) Die Funktion ![$ f_3:]-\infty;0[ $ $ f_3:]-\infty;0[ $](/teximg/6/1/00388716.png)  ![$ ]0;\infty[ $ $ ]0;\infty[ $](/teximg/7/1/00388717.png) definiert durch definiert durch  ist sowohl injektiv als auch surjektiv, also bijektiv. ist sowohl injektiv als auch surjektiv, also bijektiv.
4.) Die Funktion ![$ f_4:]0;\infty[ $ $ f_4:]0;\infty[ $](/teximg/9/1/00388719.png) 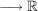 definiert durch definiert durch  ist injektiv, jedoch nicht surjektiv (also insbesondere nicht bijektiv). ist injektiv, jedoch nicht surjektiv (also insbesondere nicht bijektiv).
5.) Die Funktion  definiert durch definiert durch  ist injektiv und surjektiv, also bijektiv. ist injektiv und surjektiv, also bijektiv.
6.) Die Funktion  definiert durch definiert durch 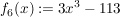 ist injektiv, jedoch nicht surjektiv (also insbesondere nicht bijektiv). ist injektiv, jedoch nicht surjektiv (also insbesondere nicht bijektiv).
7.) Die Funktion 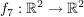 definiert durch definiert durch 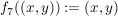 ist injektiv und surjektiv, also bijektiv. ist injektiv und surjektiv, also bijektiv.
Denn:
a) Sind 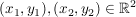 mit mit 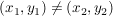 , so gilt: , so gilt:
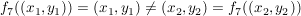 . .
Also ist 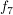 injektiv. injektiv.
b) Ist 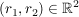 , so gilt: , so gilt:
 . .
Also ist  (hier: auch) ein Element des Definitionsbereiches mit (hier: auch) ein Element des Definitionsbereiches mit 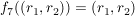 , und daher ist , und daher ist 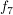 surjektiv. surjektiv.
Da 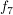 injektiv und surjektiv ist, ist injektiv und surjektiv ist, ist 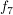 bijektiv. bijektiv.
8.) Die Funktion 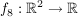 definiert durch definiert durch 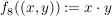 ist surjektiv, aber nicht injektiv (also insbesondere nicht bijektiv). ist surjektiv, aber nicht injektiv (also insbesondere nicht bijektiv).
Denn:
a) 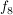 ist nicht injektiv, da: ist nicht injektiv, da:
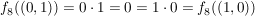 , aber , aber 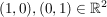 mit mit 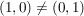 . .
b) 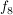 ist surjektiv: ist surjektiv:
Ist 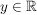 beliebig, aber fest, so gilt etwa für den Punkt beliebig, aber fest, so gilt etwa für den Punkt 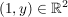 : :
 . .
Da 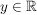 beliebig war, ist beliebig war, ist 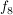 surjektiv. surjektiv.
9.) Sei 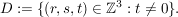 Die Funktion Die Funktion  definiert durch definiert durch 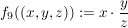 ist surjektiv, nicht aber injektiv (also auch nicht bijektiv). ist surjektiv, nicht aber injektiv (also auch nicht bijektiv).
Denn:
Wir stellen fest, dass für 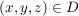 stets stets  gilt und damit insbesondere gilt und damit insbesondere 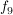 wohldefiniert ist. wohldefiniert ist.
Weiter gilt:
a) Es sind 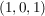 , , mit mit  , aber: , aber:
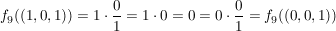 . .
Also ist 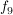 nicht injektiv. nicht injektiv.
b) 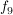 ist surjektiv. Sei dazu ist surjektiv. Sei dazu 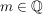 beliebig, aber fest. Dann gibt es eine Darstellung beliebig, aber fest. Dann gibt es eine Darstellung 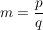 mit einem mit einem 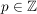 , , 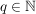 (wobei (wobei 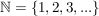 ). ).
Wegen 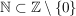 gilt also: gilt also:
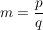 mit einem mit einem 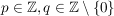 . .
Damit gilt:
 und es folgt: und es folgt:
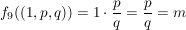 . .
Da 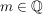 beliebig war, folgt die Behauptung. beliebig war, folgt die Behauptung.
Bemerkungen.
1.) Wie man an den ersten drei Beispielen sieht, hängt es wesentlich von dem Definitions- bzw. dem Zielbereich ab, ob eine Funktion injektiv bzw. surjektiv ist. Das ergibt sich auch sofort aus den Definitionen.
2.) Genau dann, wenn eine Funktion bijektiv (also injektiv und surjektiv) ist, existiert eine Umkehrfunktion.
3.) Mit Worten beschrieben:
Eine Funktion  heißt: heißt:
- injektiv, wenn zwei voneinander verschiedene Elemente aus dem Definitionsbereich stets auch auf zwei voneinander verschiedene Elemente des Zielbereiches abgebildet werden
- surjektiv, wenn für jedes Element des Zielbereiches ein Element im Definitionsbereich so existiert, dass dieses Element des Definitionsbereiches durch  auf das Element des Zielbereiches abgebildet wird auf das Element des Zielbereiches abgebildet wird
4.) Die Bijektivität einer Funktion  läßt sich auch so charakterisieren: läßt sich auch so charakterisieren:
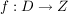 ist bijektiv ist bijektiv 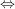 Für alle Für alle 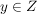 existiert genau ein existiert genau ein 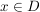 mit mit  . .
Beweis:
"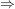 :" :"
Sei 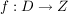 bijektiv. Ist bijektiv. Ist 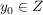 beliebig, so existiert wegen der Surjektivität von beliebig, so existiert wegen der Surjektivität von  ein ein 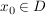 mit mit  . .
Ist 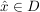 mit mit 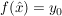 , so gilt: , so gilt:
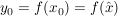 , ,
und da  injektiv ist, folgt: injektiv ist, folgt:
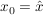 . .
Also existiert zu 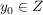 genau ein genau ein 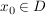 mit mit  . .
Da 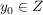 beliebig war, folgt die Behauptung. beliebig war, folgt die Behauptung.
"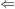 ": ":
Existiere nun zu jedem 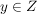 genau ein genau ein 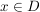 mit mit  . .
Dann ist  surjektiv (denn insbesondere existiert zu jedem surjektiv (denn insbesondere existiert zu jedem 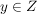 (mindestens) ein (mindestens) ein 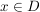 mit mit  ). ).
Angenommen,  sei nicht injektiv. Dann gibt es sei nicht injektiv. Dann gibt es 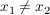 , , 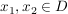 mit mit 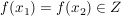 . Das heißt aber, dass es zu . Das heißt aber, dass es zu  (mindestens) zwei voneinander verschiedene Elemente in (mindestens) zwei voneinander verschiedene Elemente in 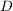 gibt, deren Bild unter gibt, deren Bild unter  gerade gerade 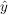 ist. Widerspruch! (Denn es kann nach Vorraussetzung nur genau eines geben!) ist. Widerspruch! (Denn es kann nach Vorraussetzung nur genau eines geben!)
Also ist  injektiv und surjektiv, und damit bijektiv. injektiv und surjektiv, und damit bijektiv. 
|